General Equation of a Line

The vertices of a triangle $∆OBC$ are $O \left(0, 0\right), B\left(-3, -1\right), C\left(-1, -3\right)$ find the equation of the line parallel to $BC$ and intersecting the sides $OB \& OC$, whose perpendicular distance from the point $\left(0, 0\right)$ is half.

Equation of the line passing through $(1,2)$ and parallel to the line $y=3x-1$ is

A  new airport, $S$ is to be constructed at some point along a straight road, $R$, such that its distance from a nearby town, $T$, is the shortest possible.

The town, $T$, and the road, $R$, are placed on a coordinate system where $T$ has coordinates $(80, 140)$ and $R$ has equation $y=x-80$. All coordinates are given in kilometres.

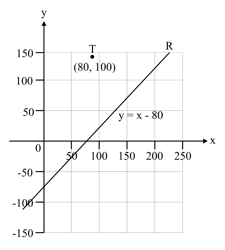
Determine the coordinates of $S$, the new airport.

Lines $L_1$ and $L_2$ are given by the equations  $L_1:ax-3y=9$ and $L_2:y=\frac{2}{3}x+4.$

The two lines are perpendicular.Hence, determine the coordinates of the intersection point of the lines.

Lines $L_1$ and $L_2$ are given by the equations  $L_1:ax-3y=9$ and $L_2:y=\frac{2}{3}x+4.$

The two lines are perpendicular. Find the value of $a.$

The coordinates of point $P$ are $\left(-3, 8\right)$ and the coordinates of point $Q$ are $\left(5, 3\right)$. $M$ is the midpoint of $\left[PQ\right]$.

$L_1$ is the line which passes through $P$ and $Q$.

The line $L_2$ is perpendicular to $L_1$ and passes through $M$.

Write down the gradient of $L_2$.

The line $L$ has equation $y=3x-5$. For the line $x+3y+9=0$, State with reasons whether they are parallel to $L$, perpendicular to $L$, or neither.

The line $L$ has equation $y=3x-5$. For the line $y=\frac{-1}{3}x+4$, State with reasons whether they are parallel to $L$, perpendicular to $L$, or neither.

The line $L$has equation $y=3x-5$. For the line $y-5=2(x-7)$, State with reasons whether they are parallel to $L$, perpendicular to $L$, or neither.

The line $L$ has equation $y=3x-5$. For the line$-6x+2y+8=0$,  State with reasons whether they are parallel to $L$, perpendicular to $L$, or neither.

The line $L$ has equation $y=3x-5$. For the line given  $y=\frac{1}{3}x-7$,  State with reasons whether they are parallel to $L$, perpendicular to $L$, or neither.

A fish farm builds a breeding basin in the form of a quadrilateral $ABCD$, with $\mathrm{A}\left(-3,-1\right),\mathrm{B}\left(2,0\right),\mathrm{C}\left(5,3\right)\text{ and }\mathrm{D}\left(0,2\right)$. Show that the quadrilateral $ABCD$ is a parallelogram.

A straight connecting street segment is built perpendicular to an existing street with equation $y=\frac{2}{7}x+3$. Determine the equation of the line of the new street segment, which passes through point $\mathrm{B}(-1,-0.2)$.

A ski resort is building two parallel straight ski slopes for children. One of them has a gradient of $\frac{1}{3}$. The other ski slope will pass through points $\left(2,-3\right)$ and $\left(s,-5\right)$. Find the value of $s$.

Determine whether the straight air routes with equations $x-\frac{y}{2}=-3$, and $x=-5$ are intersecting or not. If they are intersecting, find the point of intersection.

$L_1$ and $L_2$ are the trajectories of two ships moving in straight lines. Determine whether the ships' trajectories are perpendicular, parallel or neither:

Line $L_1$ has equation $y=-\frac{2}{5}x-1$, and line $L_2$ has equation $x-\frac{y}{3}=4$.

$L_1$ and $L_2$ are the trajectories of two ships moving in straight lines. Determine whether the ships' trajectories are perpendicular, parallel or neither:

Line $L_1$ has equation $2y-\frac{1}{2}x+3=0$, and line $L_2$ has equation $y-3=0.25(x-1)$.